代码随想录：二叉树

二叉树

[TOC]

101. Symmetric Tree

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

Example 1:

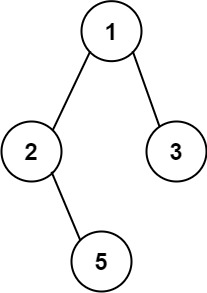
Input: root = [1,2,2,3,4,4,3]
Output: true

Example 2:

Input: root = [1,2,2,null,3,null,3]
Output: false

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• -100 <= Node.val <= 100

Follow up: Could you solve it both recursively and iteratively?

Yes ! I can

recursively

比较是否对称可以细化为，比较根节点的左右孩子，以及比较左孩子的左孩子跟右孩子的右孩子和左孩子的右孩子跟右孩子的左孩子

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
        public boolean isSymmetric(TreeNode root) {
           if(root==null) return true;
           return compareTree(root.left,root.right);
        }
        public boolean compareTree(TreeNode left,TreeNode right){
            if(left!=null&&right==null) return false;
            else if (left==null&&right!=null) return false;
            else if (left==null&&right==null) return true;
            else if (left.val!=right.val) return false;
            boolean outside = compareTree(left.left,right.right);
            boolean inside = compareTree(left.right,right.left);
            return outside&&inside;
        }
}

iteratively

使用迭代法。队列以及栈都可以使用，我们只需要成对进行push以及pop然后比较即可

Queue

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
          public boolean isSymmetric(TreeNode root) {
           if(root==null) return true;
           Queue<TreeNode> queue = new LinkedList<>();
           queue.offer(root.left);
           queue.offer(root.right);
           while(!queue.isEmpty()){
               TreeNode leftNode = queue.poll();
               TreeNode rightNode = queue.poll();
               if(leftNode==null&&rightNode==null) continue;
               if(leftNode==null||rightNode==null||leftNode.val!=rightNode.val) return false;
               queue.offer(leftNode.left);
               queue.offer(rightNode.right);
               queue.offer(leftNode.right);
               queue.offer(rightNode.left);
           }
           return true;
        }
}

Stack

class Solution {
         public boolean isSymmetric(TreeNode root) {
           if(root==null) return true;
          Stack<TreeNode> stack = new Stack<>();
           stack.push(root.left);
            stack.push(root.right);
           while(!stack.isEmpty()){
               TreeNode leftNode = stack.pop();
               TreeNode rightNode = stack.pop();
               if(leftNode==null&&rightNode==null) continue;
               if(leftNode==null||rightNode==null||leftNode.val!=rightNode.val) return false;
               stack.push(leftNode.left);
               stack.push(rightNode.right);
               stack.push(leftNode.right);
               stack.push(rightNode.left);
           }
           return true;
    }
}

104. Maximum Depth of Binary Tree

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

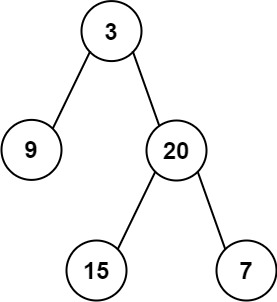
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -100 <= Node.val <= 100

DFS

class Solution {
    public int maxDepth(TreeNode root) {
      if(root==null) return 0;
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        return Math.max(left,right)+1;
    }
}

BFS

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null) {
            return 0;
        }
        deeply
        LinkedList<TreeNode> queue=new LinkedList<>();
        queue.offer(root);
        int depth=0;
        while(!queue.isEmpty()){
            int size=queue.size();
            while(size>0){
               TreeNode curr= queue.poll();
                if(curr.left!=null){
                    queue.offer(curr.left);
                }
                if(curr.right!=null){
                    queue.offer(curr.right);
                }
                size--;//剪掉一个根节点
            }
            depth++;//走完一层
        }
        return depth;
    }
}

559. Maximum Depth of N-ary Tree

Given a n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: 3

Example 2:

Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: 5

Constraints:

• The total number of nodes is in the range [0, 104].
• The depth of the n-ary tree is less than or equal to 1000.

DFS

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
     public int maxDepth(Node root) {
            if(root==null) return 0;
            int max = 0;
            for(Node child:root.children){
                max = Math.max(max,maxDepth(child));
            }
            return max+1;
        }
}

BFS

class Solution {
    public int maxDepth(Node root) {
            if(root==null) return 0;
            Queue<Node> queue = new LinkedList<>();
            queue.offer(root);
            int depth = 0;
            while (!queue.isEmpty()){
                depth++;
                int size =queue.size();
                while(size>0){
                    size--;
                    Node poll = queue.poll();
                    for (Node child : poll.children) {
                        if(child!=null){
                            queue.offer(child);
                        }
                    }
                }
            }
            return depth;
        }
}

111. Minimum Depth of Binary Tree

已解答

简单

相关标签

相关企业

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 2

Example 2:

Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5

Constraints:

• The number of nodes in the tree is in the range [0, 105].
• -1000 <= Node.val <= 1000

BFS

/**
   * Definition for a binary tree node.
   * public class TreeNode {
   *     int val;
   *     TreeNode left;
   *     TreeNode right;
   *     TreeNode() {}
   *     TreeNode(int val) { this.val = val; }
   *     TreeNode(int val, TreeNode left, TreeNode right) {
   *         this.val = val;
   *         this.left = left;
   *         this.right = right;
   *     }
   * }
   */
  class Solution {
      int min=0;
      public int minDepth(TreeNode root) {
          if(root==null){
              return 0;
          }
          LinkedList<TreeNode> queue=new LinkedList<>();
          queue.offer(root);
          while(!queue.isEmpty()){
              min++;
              int size=queue.size();
              while(size>0){
                  TreeNode p = queue.poll();
                  if(p.left!=null){
                      queue.offer(p.left);
                  }
                  if(p.right!=null){
                      queue.offer(p.right);
                  }
                  if(p.right==null&&p.left==null){
                      return min;
                  }
                  size--;
              }
          }
          return min;
      }
  }

DFS

只有左右孩子都为空时才算深度

class Solution {
    public int minDepth(TreeNode root) {
    		if(root==null) return 0;
            if(root.left==null&& root.right==null) return 1;
            if(root.left==null) return minDepth(root.right)+1;
            if(root.right==null) return minDepth(root.left)+1;
            int left = minDepth(root.left);
            int right = minDepth(root.right);
            return Math.min(left,right)+1;
    }
}

222. Count Complete Tree Nodes

Given the root of a complete binary tree, return the number of the nodes in the tree.

According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

Design an algorithm that runs in less than O(n) time complexity.

Example 1:

Input: root = [1,2,3,4,5,6]
Output: 6

Example 2:

Input: root = []
Output: 0

Example 3:

Input: root = [1]
Output: 1

Constraints:

• The number of nodes in the tree is in the range [0, 5 * 104].
• 0 <= Node.val <= 5 * 104
• The tree is guaranteed to be complete.

SimpleTree way

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        if(root==null) return 0;
        queue.offer(root);
        int ant = 0;
        while(!queue.isEmpty()){
            int size = queue.size();
            while(size>0){
                size--;
                TreeNode poll = queue.poll();
                ant++;
                if(poll.left!=null) queue.offer(poll.left);
                if(poll.right!=null) queue.offer(poll.right);
            }
        }
        return ant;
    }
}

CompleteTree way

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
       if(root==null) return 0;
       int leftDepth = 0;
       int rightDepth = 0;
       TreeNode leftNode = root.left;
       TreeNode rightNode = root.right;
       while(leftNode!=null){
        leftDepth++;
        leftNode = leftNode.left;
       }
       while(rightNode!=null){
        rightDepth++;
        rightNode = rightNode.right;
       }
       if(leftDepth==rightDepth){
        return (2<<leftDepth)-1;
       }
       int left = countNodes(root.left);
       int right = countNodes(root.right);
       return left+right+1;
    }
}

110. Balanced Binary Tree

Given a binary tree, determine if it is

height-balanced

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• -104 <= Node.val <= 104

recursively

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        return getDepth(root,0)!=-1;
    }
    public int getDepth(TreeNode root,int depth){
        if(root==null){
            return 0;
        }
        int leftDepth = getDepth(root.left,1);
        if(leftDepth==-1) return -1;
        int rightDepth = getDepth(root.right,1);
        if(rightDepth==-1) return -1;
        if(Math.abs(leftDepth-rightDepth)>1){
            return -1;
        }else{
            int midleDepth = Math.max(leftDepth,rightDepth)+1;
            return midleDepth;
        }
    }
}

257. Binary Tree Paths

Given the root of a binary tree, return all root-to-leaf paths in any order.

A leaf is a node with no children.

Example 1:

Input: root = [1,2,3,null,5]
Output: ["1->2->5","1->3"]

Example 2:

Input: root = [1]
Output: ["1"]

Constraints:

• The number of nodes in the tree is in the range [1, 100].
• -100 <= Node.val <= 100

class Solution {

        public List<String> binaryTreePaths(TreeNode root) {
           List<Integer> pathList = new LinkedList<>();
           List<String> resultList = new ArrayList<>();
           if(root==null) return resultList;
           getPathToChild(root,pathList,resultList);
           return resultList;
        }
        public void getPathToChild(TreeNode root,List<Integer> pathList,List<String> resultList){
            pathList.add(root.val);
            if(root.left==null&&root.right==null){
                StringBuilder temp = new StringBuilder();
                for (int i = 0; i < pathList.size()-1; i++) {
                 temp.append(pathList.get(i)).append("->");
                }
                temp.append(pathList.get(pathList.size()-1));
                resultList.add(temp.toString());
            }
            if(root.left!=null) {
                getPathToChild(root.left,pathList,resultList);
                pathList.remove(root.val);
            }
            if(root.right!=null){
                getPathToChild(root.right,pathList,resultList);
                pathList.remove(root.val);
            }
        }
    }

404. Sum of Left Leaves

Given the root of a binary tree, return the sum of all left leaves.

A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 24
Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.

Example 2:

Input: root = [1]
Output: 0

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• -1000 <= Node.val <= 1000

recursively

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root==null){
            return 0;
        }
        if(root.left==null&&root.right==null){
            return 0;
        }
        int left = sumOfLeftLeaves(root.left);
        if(root.left!=null&&root.left.left==null&&root.left.right==null){
            left =  root.left.val;
        } 
        int right = sumOfLeftLeaves(root.right);
        int sum = left + right;
        return sum;
    }
}

iteratively

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root==null){
            return 0;
        }
        if(root.left==null&&root.right==null){
            return 0;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        int sum = 0 ;
        while(!stack.isEmpty()){
            TreeNode top =  stack.pop();
            if(top.left!=null&&top.left.left==null&&top.left.right==null){
                sum += top.left.val;
            }
            if(top.right!=null) stack.push(top.right);
            if(top.left!=null) stack.push(top.left);
        }
        return sum;
    }
}

513. Find Bottom Left Tree Value

Given the root of a binary tree, return the leftmost value in the last row of the tree.

Example 1:

Input: root = [2,1,3]
Output: 1

Example 2:

Input: root = [1,2,3,4,null,5,6,null,null,7]
Output: 7

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -231 <= Node.val <= 231 - 1

Queue (BFS)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int findBottomLeftValue(TreeNode root) {
        if(root==null){
            return 0 ;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int left = 0;
        while(!queue.isEmpty()){
            TreeNode leftNode = queue.getFirst();
            left = leftNode.val;
            int size = queue.size();
            while(size>0){
                TreeNode cur = queue.poll();
                if(cur.left!=null) queue.offer(cur.left);
                if(cur.right!=null) queue.offer(cur.right);
                size--;   
            }
        }
        return left;

    }
}

iteravely

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int maxDepth = 0;
    int result = 0;
    public int findBottomLeftValue(TreeNode root) {
        if(root==null){
            return 0;
        }
        iteravely(root,1);
        return result;
    }
    public void iteravely(TreeNode root,int depth){
        if(root.left==null&&root.right==null){
            if(depth>maxDepth){
                result =root.val;
                maxDepth = depth;
            }
        }
        if(root.left!=null){
            depth++;
            iteravely(root.left,depth);
            depth--;
        }
        if(root.right!=null){
            depth++;
            iteravely(root.right,depth);
            depth--;
        }
    }

}

112. Path Sum

Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.

A leaf is a node with no children.

Example 1:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
Explanation: The root-to-leaf path with the target sum is shown.

Example 2:

Input: root = [1,2,3], targetSum = 5
Output: false
Explanation: There are two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.

Example 3:

Input: root = [], targetSum = 0
Output: false
Explanation: Since the tree is empty, there are no root-to-leaf paths.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null){
            return false;
        }
        Stack<TreeNode> stack = new Stack<>();
        Stack<Integer> sumStack = new Stack<>();
        sumStack.push(root.val);
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode top = stack.pop();
            int sum = sumStack.pop();
            if(sum == targetSum&&top.right==null&&top.left==null) return true;
            if(top.right!=null){
                stack.push(top.right);
                sumStack.push(sum+top.right.val);
            }
            if(top.left!=null){
                stack.push(top.left);
                sumStack.push(sum+top.left.val);
            }
        }
        return false;
    }
}

113. Path Sum II

Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where the sum of the node values in the path equals targetSum. Each path should be returned as a list of the node values, not node references.

A root-to-leaf path is a path starting from the root and ending at any leaf node. A leaf is a node with no children.

Example 1:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]
Explanation: There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22

Example 2:

Input: root = [1,2,3], targetSum = 5
Output: []

Example 3:

Input: root = [1,2], targetSum = 0
Output: []

(1)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 class Solution {
        List<List<Integer>> resultList = new ArrayList<>();
        List<Integer> pathList = new ArrayList<>();

        public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
            resultList.clear();
            pathList.clear();
            if(root==null) return resultList;
            pathList.add(root.val);
            traversal(root,targetSum - root.val);
            return resultList;
        }
        public void traversal(TreeNode root, int ant){
            if(root.right==null&&root.left==null&&ant==0){
                resultList.add(new ArrayList<>(pathList)); // !!
                return;
            }
            if(root.right==null&&root.left==null) return;
            if(root.left!=null){
                pathList.add(root.left.val);
                ant -= root.left.val;
                traversal(root.left, ant);
                ant += root.left.val;
                pathList.remove(pathList.size()-1);
            }
            if(root.right!=null){
                pathList.add(root.right.val);
                ant -= root.right.val;
                traversal(root.right, ant);
                ant += root.right.val;
                pathList.remove(pathList.size()-1);
            }
        }
    }

(2) 好好品

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 class Solution {
        List<List<Integer>> resultList ;
        List<Integer> pathList ;

        public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
            resultList = new ArrayList<>();
            pathList = new LinkedList<>();
            if(root==null) return resultList;
            traversal(root,targetSum);
            return resultList;
        }
        public void traversal(TreeNode root, int ant){
            if(root==null) return;
            pathList.add(root.val);
            ant -= root.val;
            if(root.right==null&&root.left==null&&ant==0){
                resultList.add(new LinkedList<>(pathList));
            }
            traversal(root.left, ant);
            traversal(root.right, ant);
            pathList.removeLast();
        }
    }